Crossover Rate

Crossover rate is the cost of capital where two projects have the same net present values (NPV) or where their NPV profiles intersect. This calculation is often used in analyzing capital budgets as it offers insights about the cost of capital if two mutually exclusive projects are as good as each other. If the cost of capital is higher than the crossover rate, the relative preferability of the projects is affected. 

For example, if project 1 is more favorable at a discount rate lower than the crossover rate, project 2 becomes viable once the cost of capital exceeds the crossover rate.

A crucial factor in computing the crossover rate is the net present value (NPV), which is obtained by calculating the present value (PV) of a project’s total costs and revenues and discounting it to align future cash flows. Many companies use net present value profiles or graphs to help them make decisions.

Another important factor in calculating the crossover rate is the internal rate of return (IRR), also called rate of return (ROR) or discounted cash-flow rate of return (DCFROR). The IRR is the discount rate when certain cash flows have an NPV of exactly zero. The IRR is often used as a profitability metric, and a higher IRR indicates greater growth potential for a project.

Crossover Rate Formula

So, we know that the point where the NPV of the two projects intersect is the crossover rate. So how do we calculate it?

One way is to calculate the NPV of each project and then solve for the interest rate. The first project has three cash flows at the end of years 1, 2, and 3, with an initial capital investment of A:

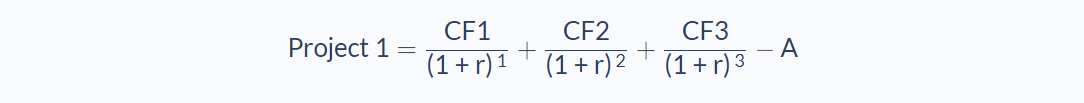
The second project has expected cash flows of CF_iii at the end of year 3, with an initial capital investment of B:

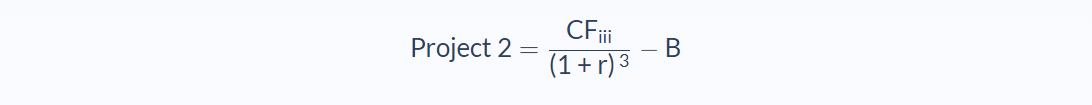
So in this case, the crossover point formula would be:

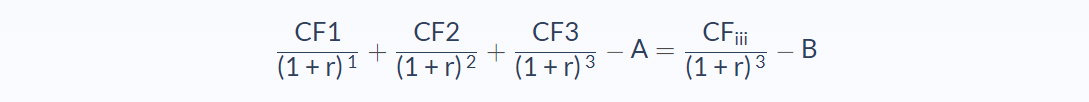
It might seem complicated at first glance, but we really just need to find the correct rate (r) that makes the equation true.

There is an easier and shorter way to calculate the crossover point using the internal rate of return.

In the example below, we’ll go through the following process:

1. Calculate the stream of cash flows for the two projects
2. Work out the difference between the initial investments and cash flows
3. Calculate the IRR of the result

Basically, the difference between the two projects becomes a new project that you calculate the IRR on. That value is your crossover rate.

Crossover Rate Example

Severson Construction is planning to undertake two ventures. The projected cost for Project A is $25 million and the expected cash flows at the end of each year for three years are $30 million, $20 million and $10 million, respectively. On the other hand, Project B is expected to cost $40 million and earn $125 million at the close of the third year. What is the crossover rate for the two projects?

Our values for this crossover rate comparison are (in thousands):

• Initial investment: ($25,000) – ($40,000) = $15,000
• Year 1: $30,000 – $0 = $30,000
• Year 2: $20,000 – $0 = $20,000
• Year 3: $10,000 – $125,000 = ($115,000)

We can now add these values to the IRR formula:

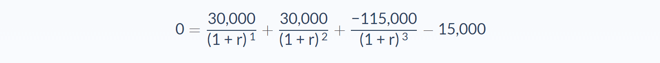
Now you just need to solve for r using your financial calculator. For this example, we’ll solve it with a simple Excel spreadsheet:

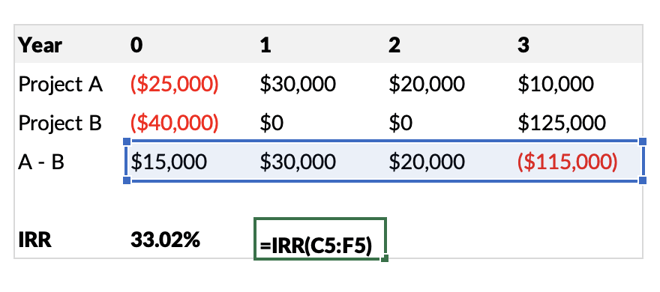
In this case, Projects A and B would have a crossover rate of 33.02%.

Project B appears to be more attractive as the cost of capital is under 33%. Should the cost of capital go higher than 33%, Project A will have a higher NPV and thus be more favorable.

Crossover Rate Analysis 

The crossover rate determines which of the two potential projects is more profitable. Specifically, the calculation offers insight into the performance of different projects and weighs their potential earnings against risks.

To calculate the IRR, the same formula is used as the NPV. However, the NPV is substituted with zero and the IRR takes the place of the discount rate. Also, unlike the NPV, the IRR comes with the assumption that a project’s positive cash flows are all reinvested into the IRR rather than the cost of capital. The formula takes for granted that positive cash flows are returned into the IRR.

With an NPV of exactly zero, the IRR will return the cost of capital of a project. So if the cost of capital is 8.5% and that project’s NPV returns zero, the IRR will automatically be 8.5% for that project. Hence, all the cash inflows’ present value will only be sufficient for the cost of capital. An NPV of zero or an IRR below the cost of capital also means zero value for the shareholders. 

Another advantage of the IRR is the fact that it accounts for the time value of money, and the cash flow’s economic life. However, IRR cannot scale shareholders’ value nor can they be added. So if there are three projects whose IRRs are 10%, 13%, and 22%, the total IRR is not necessarily 45%. All the projects’ cash flows will be combined instead to determine the correct IRR, and just like the NPV, the IRR does not provide any hints of the original investment’s size. 

Lastly, IRR cannot be calculated with entirely positive or negative cash flows when the original investment is greater than the total of undiscounted revenues, or when differences in cumulative cash flow streams sign at least twice by shifting from positive to negative.

Crossover Rate Conclusion

• The crossover rate is the cost of capital at which two projects are of equal net present values (NPV) or with intersecting NPV profiles.
• The crossover rate formula requires two variables: Initial Investments (for the two projects) and Cash Flows (from one period to the next).
• The crossover rate is usually expressed as a percentage.
• The crossover rate is used by companies to know which of the two projects is more favorable.

Crossover Rate Calculator

You can download the crossover rate calculator Excel template below to quickly determine the crossover rate between two projects, by entering the required numbers.

Click here to download the template

FAQs

1. What does crossover rate mean?

The crossover rate is the cost of capital at which two projects are of equal Net Present Value.

2. How do you calculate the crossover rate?

To calculate the crossover rate, you must have two projects and a single cash flow stream for each project.

3. Is the crossover rate the same as IRR?

No, the crossover rate is not the same as IRR. The cross-over rate is the cost of capital at which two projects are of equal Net Present Value while IRR is the Internal Rate of Return that must be used for a single cash flow stream.

4. What is a crossover chart?

A crossover chart speeds up the process of identifying those projects which have a crossover rate. A crossover chart uses a graph to plot two IRR curves and determine where they cross..

5. What is the crossover point?

The crossover point is the intersection of two IRR curves when both projects have a positive value.