Net present value (NPV) is the difference between the present value of cash inflows and outflows of an investment over a period of time. Put simply, NPV is used to work out how much money an investment will generate compared with the cost adjusted for the time value of money (one dollar today is worth more than one dollar in the future).
Net present value is used in capital budgeting and investment planning so that the profitability of a project or investment can be analyzed. This is important because it factors in the time value of money and the associated interest and opportunity costs.
Savvy investors and company management will use some form of present value or discounted cash flow calculation like NPV when making important investment decisions.
Net Present Value Formula
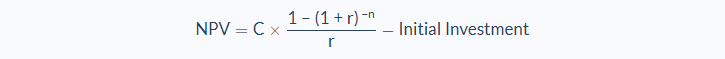
- C = net cash inflow per period
- r = rate of return (also known as the hurdle rate or discount rate)
- n = number of periods
In this formula, it is assumed that the net cash flows are the same for each period. However, if the payments are not even, the formula is a little more complicated because we need to calculate the present value of each individual net cash inflow.
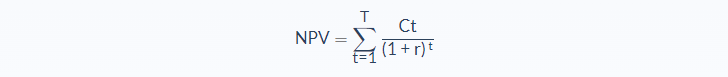
- Ct = net cash inflow per period during a single period
- r = rate of return
- t = number of time periods
The formula looks complicated to take account for all of the future cash flows and discount them by the interest rate (r), but we can simplify it to the following so that you understand what is going on:

So in this simplified net present value formula, we work out the NPV by subtracting the PV of the initial investment from the PV of the future cash flows from the investment. Put simply, this discounts the future value over the length of the investment by subtracting the current dollars needed to purchase the investment, so that investors can see the true net return of the investment.
Net Present Value Example
Henry Construction Co specializes in small commercial buildings but the owner, Henry, wants to expand into larger buildings by purchasing a larger crane for $100,000. He estimates that for the next 10 years he will be able to earn at least $20,000 from the new purchase.
The maths looks good. Henry invests $100k and gets $200k over the next ten years. However, the $200,000 has not been discounted to factor in the time value of money.
Assuming an annual interest rate of 10%, the discounted cash flow of the crane investment amounts to $122,891.34. Now we can work out the NPV of the investment:
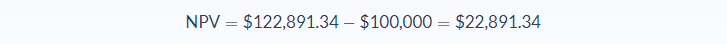
So what does this mean? In simple terms, it means that when you factor in the time value of money, the crane investment doesn’t make $100,000 ($200k-$100k), it makes a net present value of $22,891.34.
It could still be a worthwhile investment for Henry, but he would be wise to compare this NPV with other investment options to see if there are any better options for him.
Limitations of Net Present Value
When you compare NPV to other investment appraisal methods that don’t discount future cash flows – for example, accounting rate of return and payback period – the net present value can be a better approach because it accounts for the time value of money.
Even compared to other discounted cash flow techniques like the internal rate of return (IRR), the NPV is heavily favored because the net present value provides a dollar value which can form the foundation of an investment decision. IRR is more commonly calculated as part of the capital budgeting process to provide extra information.
That said, it’s always worth bearing in mind that the net present value is based on estimates and assumptions. It’s not always completely accurate. In our example above, we have no way of knowing if the interest rate will remain at 10% each year for ten years, or if the crane will actually be able to generate $20,000 a year.
For this reason, NPV should be used as an indicator and not as a true evaluation of the investment.
Net Present Value Conclusion
When calculating net present value, the below points are worth bearing in mind as a quick recap of what it is, why it’s used, and how to use it:
- The change in a company’s net worth/equity is what the net present value (NPV) of a project represents.
- Each period of the project’s projected net after-tax cash flows, initial investment outlay, and the appropriate discount rate is really important in calculating the net present value.
- Net cash flow may be considered as even or uneven.
- There are decision rules that you should consider.
- NPV has some strengths as well as weaknesses.
Net Present Value Calculator
You can use the net present value calculator below to work out the present value of an investment by entering the cash flow for each period, the discount rate, and the initial investment amount.
You can also download our NPV Excel template here.
FAQs
1. What is Net Present Value (NPV)?
NPV is the sum of all cash flows, both positive and negative, that are expected to occur over the life of a project. It takes into account not only the cash inflows and outflows but also the time value of money.
2. What is the formula for calculating Net Present Value (NPV)?
NPV = CF1 / (1+r)^1 + CF2 / (1+r)^2 + … where CF = cash flow and r = the interest rate per period of time
3. What is a good net present value?
A positive NPV means the present value of cash inflows is greater than the present value of all cash outflows. This suggests that the investment is a good one and should be undertaken.
4. What does a negative Net Present Value (NPV) number mean?
A negative NPV number suggests that the present value of cash inflows is less than the present value of all cash outflows. This would mean that the investment is not a good one and should not be undertaken.
5. What is the net present value used for?
Net present value is used to make decisions about whether or not a particular investment is worth undertaking. It takes into account the time value of money and all cash flows associated with the investment. If the NPV is positive, the investment is worthwhile. If the NPV is negative, the investment is not worthwhile.

