The present value of a growing annuity is a way to get the current value of a fixed series of cash flows that grow at a proportionate rate. In other words, it is the present value of a series of payments which grows (or declines) at a constant rate each period.
Unlike the present value of a growing perpetuity (which is an infinite series of payments) the PV of a growing annuity has a fixed number of periods.
A growing annuity can also be known as an increasing or graduated annuity. The payments are made at the end of each period for a fixed number of periods, a discount rate is applied, and the formula discounts the value of each payment back to the original value at the start of the first period (the present value).
Present Value of a Growing Annuity Formula
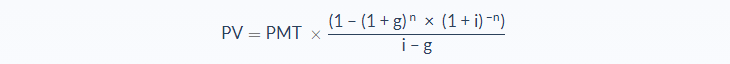
- PV = Present Value
- PMT = Periodic payment
- i = Discount rate
- g = Growth rate
- n = Number of periods
When using this formula the discount rate and the growth rate should not be equal. If the discount rate and the growth rate are equal, the formula below should be used instead:
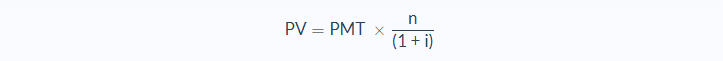
- PV = Present Value
- PMT = Periodic payment
- i = Discount rate
- n = Number of periods
Present Value of a Growing Annuity Example
Rebecca has set up a savings account with her bank and will be paying $350 a month into the account for the next five years. The annual interest rate is 3% and the annual growth rate is 2%. How can Rebecca work out the present value of these payments?
Since the interest in this example is applied annually, the number of periods (n) will be 5, and the total annual payment is $350 x 12 = $4,200.
If the interest rate was applied monthly, we would take the annual interest rates and divide them by 12 to get a monthly discount rate (i) of 0.0025% and a monthly growth rate (g) of 0.0017%, using a total number of periods (n) of 60.
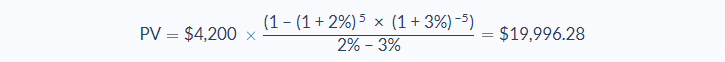
Now, what if Rebecca’s bank did pay the interest monthly instead of annually? In that case, the formula would look like this:
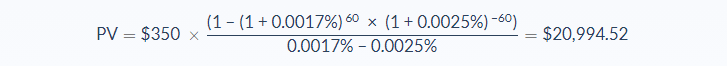
Why is the present value of the growing annuity higher when interest is applied monthly?
The PV of the annuity is growing faster because the payments are compounding 12 times a year at the 2% growth rate instead of just once a year with annual interest.
Present Value of a Growing Annuity Analysis
The PV of a growing annuity is based on the time value of money concept, which basically states that $1 today is worth more today than at a future time.
The formulas allow you to work out the present value of an annuity so that smart investors can see how much their money is worth today because money has the potential for growth over a period of time.
So let’s say you have the option to receive a payment of $10,000 today or in two years time. You would pick the first option, right? It’s the same amount of money whenever you receive it, but time is the important factor. The $10,000 received today has more value and use to you than waiting to receive it later.
There are opportunity costs to not receiving the money today, such as any potential interest you could earn over the two years.
Present Value of a Growing Annuity Calculator
You can use the present value of a growing annuity calculator below to work out your own PV using the required formula inputs.
If the growth and discount rate are the same, the calculator will use the correct formula (mentioned above). I think it may be the only PV of a growing annuity calculator to do that!
FAQs
1. What does the present value of a growing annuity mean?
The present value of a growing annuity is the amount that an individual would be willing to pay in order to receive a stream of payments for a fixed number of periods.
It can also be used to calculate the interest rate that needs to be applied in order to grow an initial sum into the sum produced by all future cash flows resulting from compounding interest.
2. What is the importance of determining the present value of the annuity?
The present value of an annuity is the amount of money required today to cover a series of future annuity payments. A sum of money received today is worth more than the same sum received at a later period due to the time value of money.
3. What is a growing annuity?
A growing annuity is a series of payments that increase over time. This increase can occur annually or monthly.
4. What does present value mean?
A present value calculation calculates what a future sum of money is worth today.
For example, if someone wants to calculate the present value of their retirement savings over 10 years, they will need to know how much money they will have in 10 years and discount it back to its present value using an interest rate.
5. What is the formula for calculating the present value of an annuity?
The formula for determining the present value of an annuity is:
PV = PMT × (1 − (1+g)n) / i - g
where:
PV = Present Value
PMT = Periodic payment
i = Discount rate
g = Growth rate
n = Number of periods

