The present value of an annuity is a series of cash installments that are made over a certain period of time. In an ordinary annuity, these payments are distributed at the end of the pay period. But if you were to put money into an annuity today, what would be the value of that money now, knowing you’ll be receiving future payments?
The word “value” here, refers to the financial limits that a series of payments can attain. The present value of an annuity is the value of money you would invest now in an annuity, directly affected by the interest and payments the annuity would make in the future.
To accomplish this, this formula accounts for what is known as the time value of money. Simply put, the money that you invest now has a greater value than the same amount of money you would invest in the future. This is because the money you invest now has a longer period of time to accumulate interest. In looking for the present value of an annuity, if you had the choice of being paid $1000 today or investing $1000 today, the value of the money invested would be higher because of its potential to gain interest.
Present Value of an Annuity Formula
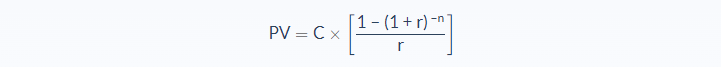
- C = cash flow per period
- r = interest rate
- n = number of periods
Occasionally, you will see that the term interest rate is sometimes referred to as a discount rate when discussing present value. It is important to pay particular attention to the rate as you are calculating this equation.
With an annuity, payments can be sent out at different intervals. You could be paid monthly, semi-annually, annually, etc. The frequency of interest rate that you use in the calculation should match the frequency of the number of payments you are using as variable n. If you are being paid monthly, then you should be using a monthly interest rate in your calculation.
For example, if you have an annuity that would send monthly payments, and you have an annual interest rate of 6%, you would use a monthly interest rate of 0.05% in your calculations.
It is important to note that, in this formula, the interest rate must remain the same through the series, and payment amounts must be equally distributed. If the amount distributed by the annuity changes or if the interest rate increases or decreases, then this formula would not apply. If the payments from the annuity will eventually increase at a particular rate, then you would use the formula for the present value of a growing annuity instead.
Present Value of an Annuity Example
Mr Fieldman is planning his estate and wants to leave his son some money. He can choose between an annuity of $50,000 paid annually at the end of each year for 25 years or a $1,000,000 lump sum. The annuity would have a 4% annual interest rate. Mr Fieldman wants to know what the present value of the annuity for his son would be compared to the one-time payment.
Let’s break it down to identify the meaning and value of the different variables in this problem.
- Number of Periods(n): 25
- Cash value of annuity payments per period (C): 50,000
- Interest rate (r): 4% or 0.04
- Future Value of an Annuity Due (FV): Unknown
We can apply the values to our formula and calculate the present value of this annuity based on his future payments.
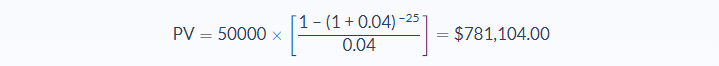
Using this equation, the present value of the annuity would be $781,104.00.
While there are other factors that Mr Fieldman can consider in deciding how to leave his son the money, he now knows what the present value of the annuity would be. He can compare it to the lump sum to see that a lower amount invested now could be more financially beneficial for his son than a lump sum.
Present Value of an Annuity Analysis
Most of the time, retirement planning will be the reason behind needing to calculate the present value of an annuity. Individuals outlining their retirement will want to know how much they need to invest today to be paid a certain amount from each payment of their annuity.
This calculation can also come in handy when working with a lottery annuity or planning an annuity for an estate, like in the example above. Annuities can be very attractive because they have the potential to provide income for the remainder of someone’s lifetime.
Additionally, having a fixed interest rate and dependable payments can remove some of the stress of retirement planning. However, it is important to remember that taxes must still be paid on the money distributed from an annuity, and additional fees can make them more costly as well.
When calculating the present value of an annuity, the initial investment needs to be one period away from the start of the annuity, or else it would change the value of the payments made in the future. If the initial investment is more than one payment period away from the start of the annuity, then you could use either the present value of an annuity due formula or the present value of a deferred annuity instead.
Present Value of an Annuity Conclusion
- The present value of an annuity formula is a tool to help plan an investment amount based on the desired cash flow later.
- Present value of an annuity due is primarily used to assess how much would need to be paid immediately into an annuity to have a specific payment amount coming from the annuity.
- In finding the present value of an annuity, the investment would need to be no more than one period before the start of the annuity.
- The payments from the annuity would come at the end of the given period.
- The formula for the present value of an annuity identifies 3 variables: the cash value of payments made by the annuity per period, the interest rate, and the number of payments within the series.
- The present value of an annuity calculation is only effective with a fixed interest rate and equal payments during the set time period.
Present Value of an Annuity Calculator
You can use the present value of an annuity calculator below to instantly work out the value of your future payments by entering the required numbers.
FAQs
1. What is the present value of an annuity?
The present value of an annuity is the lump sum amount that would need to be invested today to receive a fixed series of payments in the future.
2. What is the formula for calculating the present value of an annuity?
The present value of an annuity formula is: PV = C × [1 − (1+r) –n / r ]
3. When is the present value of annuity calculated?
The present value of an annuity is typically calculated when retirement planning or estate planning.
4. What is the difference between an ordinary annuity and an annuity due?
The primary difference between an ordinary annuity and an annuity due is that payments for an annuity due are made at the beginning of the period instead of at the end.
5. What are the benefits of the present value of an annuity?
The present value of an annuity can provide a guideline for how much needs to be invested today in order to have a specific payment amount come from the annuity in the future. Additionally, it can remove some of the stress of retirement planning. However, taxes and other fees should still be considered.
