These are additional time value of money problems using the money solution grid. For more information, make sure you review the Time Value of Money Solution Grid lesson first.
Future Value of Single Sums
Problem 1
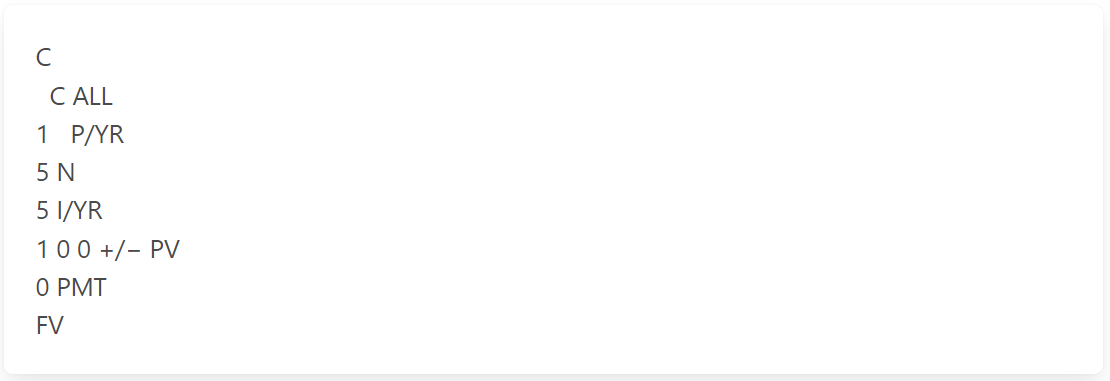
Find the future value of $100 in 5 years at 5%.
The solution grid:

The answer is: $127.63
The calculator keystrokes:
Problem 2
Find the future value of $1,800 in 3 years at 8%.

The answer is: $2,267.48
The calculator keystrokes:

Problem 3
Find the future value of $500 in 6 years at 9%.
The solution grid:

The answer is: $838.55
The calculator keystrokes:

Future Value of Annuity
Problem 1
Find the future value of a 3-year, $300 per year annuity at 6%.
The solution grid:

The answer is: $955.08
The calculator keystrokes:

Problem 2
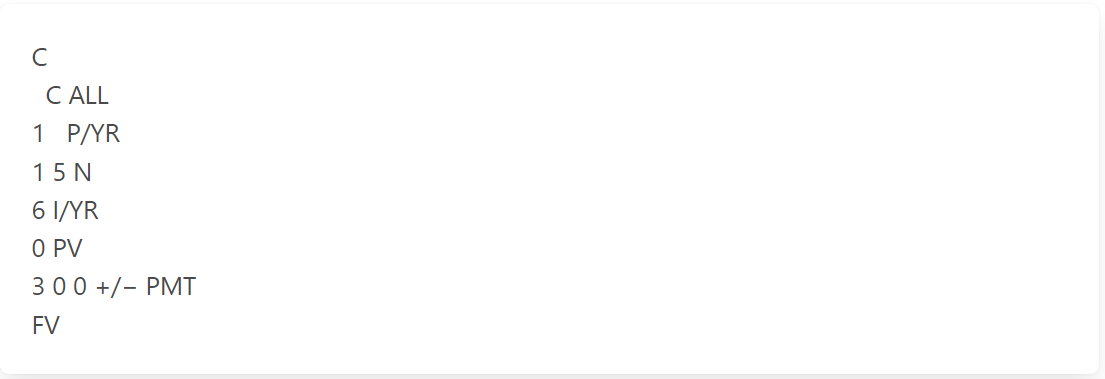
Find the future value of a 15-year, $300 per year annuity at 6%.
The solution grid:

The answer is: $6,982.79
The calculator keystrokes:
Present Value
Problem
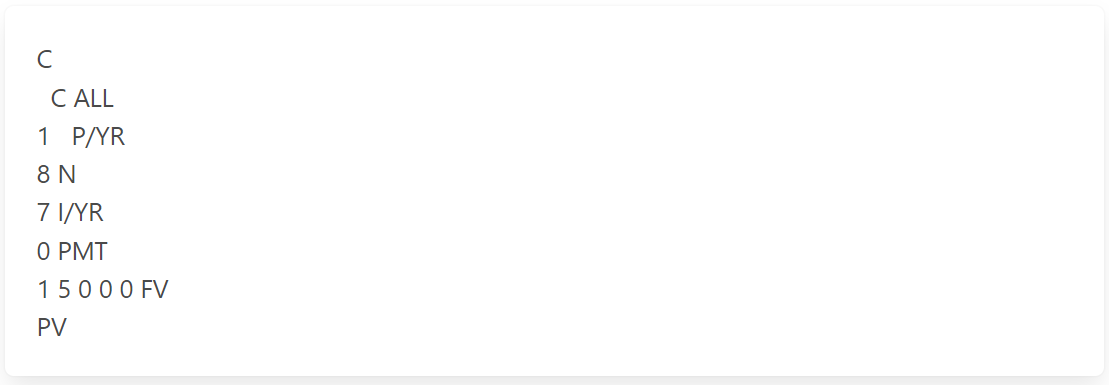
How much would you have to deposit now to have $15,000 in 8 years if interest is 7%?
The solution grid:

The answer is: $8,730.14
The calculator keystrokes:
Remember the answer is displayed as a negative value indicating that you would have a cash outflow in the present to receive a cash inflow in the future.
Present Value of Annuity
Problem
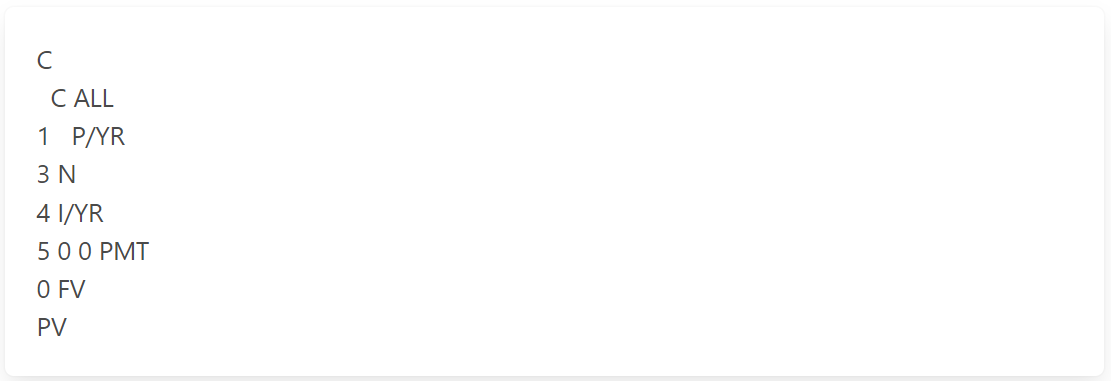
Find the present value of a 3-year, $500 annuity at 4%.
The solution grid:

The answer is: $1,387.55
The calculator keystrokes:
Again, a negative value indicates a cash outflow.
Intrayear Compounding
Problem
Find the present value of a $400 payment received every six months for 3 years.
Interest is 4%, compounded semiannually.
Number of Compounding Periods (N) = Number of Years (3) × Number of Times Per Year Compounding (2)
The solution grid:

The answer is: $2,240.57
The calculator keystrokes:
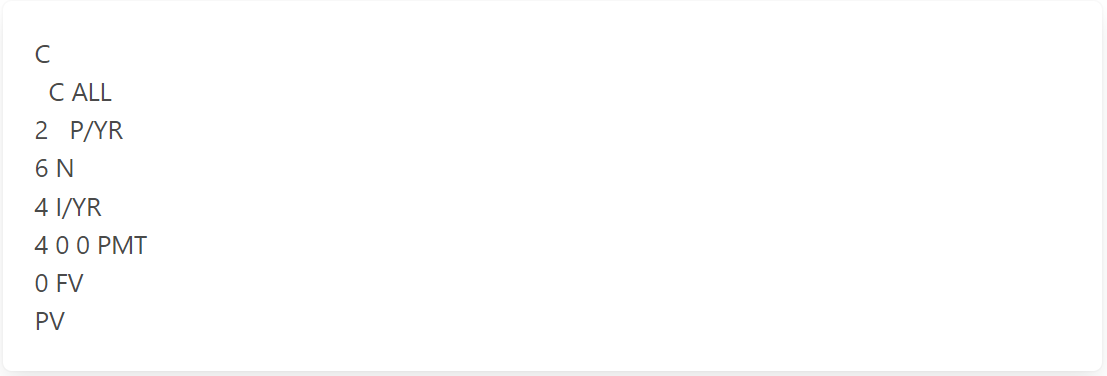
And again, a negative value.
Annuity Due
Problem
Find the future value of a 4-year annuity due of $400 at 6%.
As it is an annuity due, the calculator should be set for beginning-of-year cash flows.
The solution grid:

The answer is: $1854.84
The calculator keystrokes:
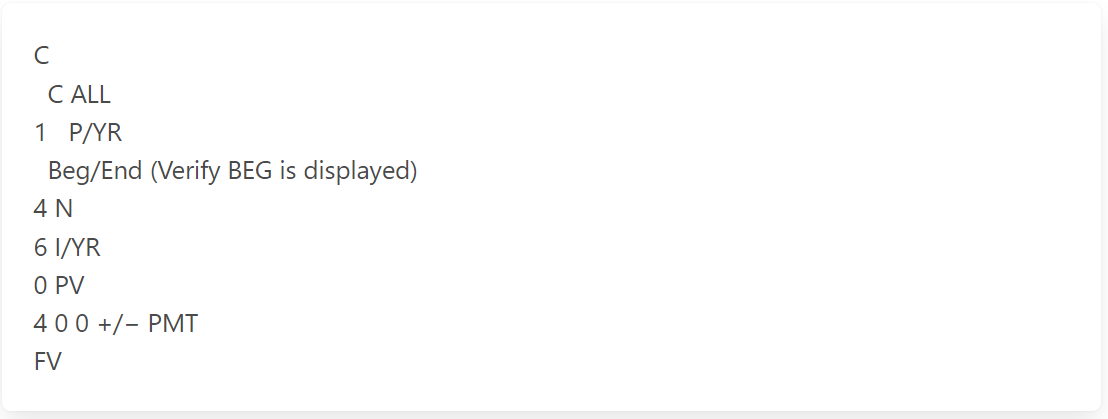
Remember to set the calculator back into End mode by pressing Beg/End until BEG clears from the calculator display.
Interest
Problem 1
If you borrow $1,000 and pay back $1,728 in three years, what annual rate of interest are you paying?
The solution grid:

The answer is: 20%
The calculator keystrokes:

Problem 2
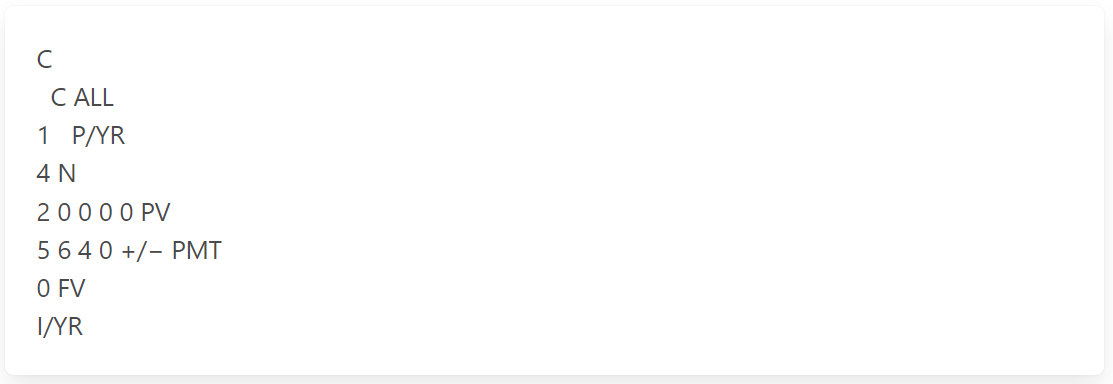
If you borrow $20,000 and pay back in four equal annual installments of $5,640,
what interest rate are you paying?
The solution grid:

The answer is: 5%
The calculator keystrokes:
Compounding Periods
Problem 1
You borrow $50,000 at 6% and agree to remit installments of $11,870 every year.
How many years will you do this?
The solution grid:

The answer is: 5 Years
The calculator keystrokes:

Problem 2
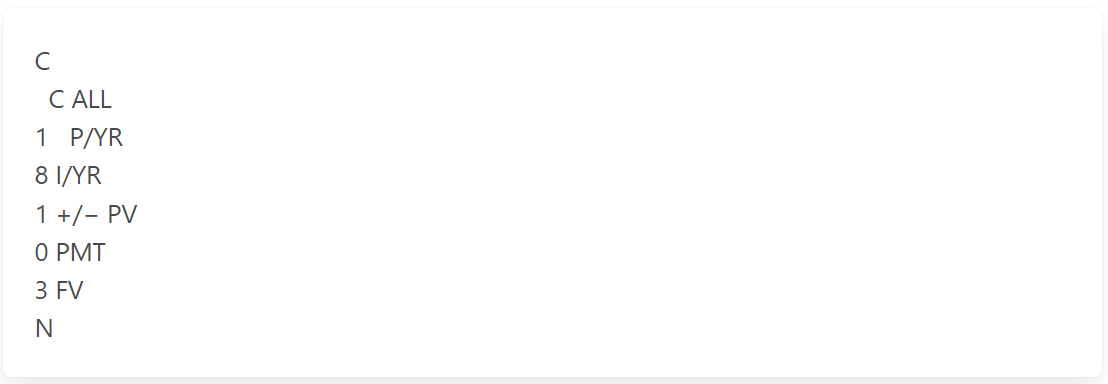
How long will it take you to triple your money at 8%?
The solution grid:

The answer is: 14.27 Years
The calculator keystrokes:
The Rule of 72
As an aside, there is a simple calculation to estimate the number of years it would take to double an investment. The Rule of 72 states that by dividing the annual interest rate into 72, the result will be an approximation of the number of years it would take for an amount to double.
For example, at 12% how long would it take to double your money?
• Rule of 72: 72 ÷ 12 = 6 years
• Using a financial calculator: 6.12 years
Solving for Payment
Problem
How much would you have to pay each year to pay off a 5%, 7-year loan of $300,000?
The solution grid:

The answer is: $51,845.95
The calculator keystrokes:

The answer displays a negative value indicating cash outflow for each payment.
This overview was developed by Dr. Sharon Garrison.
No adaptation of its content is permitted without permission.
FAQs
1. What is time value of money?
The concept that money paid or received in the future is not as valuable as money paid or received today because the money received today can be reinvested to earn interest, with the result that it has greater potential for earning an income.
2. Why is time value of money important?
The time value of money is important because it helps investors and people saving for retirement determine how to get the most out of their money.
3. How is time value of money used in decision making?
When a company makes cash flow investments, such as in a building or piece of equipment, the Time Value of Money is used to determine the present value of those cash flows.
4. What is the time value of money formula?
The Time Value of Money formula is FV = PV x [ 1 + (i / n) ] (n x t)] where V is the Future value of money, PV is the Present value of money, i is the interest rate, n is the number of compounding periods per year, and t is the number of years.
5. When to use time value of money?
Time Value of Money calculations are used when you want to determine the present values for future cash flows from investments, such as in buildings or equipment.
