TI-84 Plus TVM Tutorial

When compared to other financial calculators used on finance courses, the TI-84 is fairly easy. If you want to learn how to use its financial functions in order to handle the time value of money problems and want to easily calculate anything financial, then make sure you keep on reading.

If you’re looking for a quick recommendation for a finance calculator that will be suitable for most finance and accounting students, the calculator we recommend is the Hewlett Packard 10bII+.

(click here to find out why)

This calculator is usually around $25 on Amazon and is a good choice for business and finance needs to calculate loan repayments, interest rates, TVM, NPV, IRR, cash flows and more.

This calculator is suitable for use in the CFP exam but not the CFA exam. If you need a calculator for CFA, go for the HP 12C or the TI BAII Plus instead.

How to set up the TI 84 Plus

Before you start using TI 84 Plus, there is just one thing that you need to adjust. Since the displays of this calculator only have two decimal places by default, it’s highly recommended that you set it up into having five decimal places.

You can change the display by pressing the MODE key and then the down arrow key just once. You can then use the right arrow key so you can highlight the 5 and then press Enter. Lastly, exit the menu by pressing 2nd MODE. If you’ve done all of that successfully, congratulations! You can now start using your calculator.

In this tutorial, we will be using a lot of the TVM Solver. The TI 84 Plus, however, offers more financial functions in the Finance menu. Be sure to check the FAQ section as well.

Sample Calculations

Let’s start by working on a very simple problem that will teach you some skills and will help you solve financial math on the TI-84:

Example 1: Mark has $100 to invest for a period of 5 years with a 10% interest rate per year. Once this time period ends, how much money would Mark have accumulated?

In this problem, here are the things we know:

• The present value (PV) is $100
• N is 5
• i is 10%

Make sure that you put the calculator into the TVM Solver mode before you enter the data. Then, press the Apps button, choose the Finance menu (or you may also press the 1 key), and then choose the TVM Solver (or you may also press the 1 key).

You can then start entering the data as shown in the table below:

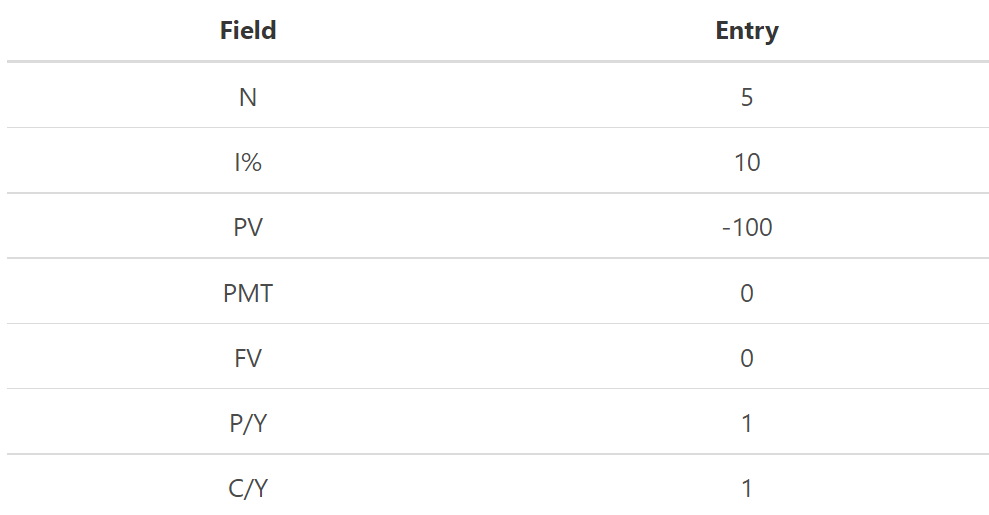
You then just have to scroll to the FV line and press Alpha Enter in order to find the future value. You should get 161.05 as an answer.

A couple of things to keep in mind:

• There are either 4 or 5 variables in every time value of money. They correspond to the 5 basic financial keys. These variables will always give you 3 or 4 and will be asked to find a solution for the other. You have a 4-variable problem and were given 3 of them  (N, I%, and PV) and were required to find a solution for the 4th (FV), in this case. You can solve these problems by simply entering the variables that you know on the correct lines and then scroll to the line for the variable you wish to find a solution with. You just have to press Alpha Enter so you can get the answer. Don’t forget to set any variables not in the problem to 0 because if you don’t, they will be included in the calculation.
• It doesn’t matter whether you entered the numbers in order or not.
• Ensure that the payments per year (P/Y) and compounding periods per year (C/Y) is set to 1. We prefer it this way. It’s not really necessary because these can be seen on the screen at all times. It will be much easier for you if you can remember to change these (1 for annual compounding, 12 for monthly compounding, etc) to the appropriate values for each problem.
• We placed 10 rather than 0.10 when we entered the interest rate. The reason for this is that the calculator automatically divides any entered number on the I% line by 100. The future would have come out to 100.501 had you entered 0.10 which is obviously not correct.
• Did you notice that we entered the 100 in PV as a negative number? We actually did that on purpose. Financial calculators mostly follow the Cash Flow Sign Convention. The reason for this is to keep the direction of the cash flow straight. Positive numbers being entered are cash inflows while negative numbers being entered are cash outflows. In the problem above, the investment was $100 and in five years, the future value of $161.05 would be a cash inflow. No harm would have been done even if you entered the $100 as a positive number but a negative number would have been the returned answer. Had you borrowed $100 today (cash inflow) and said yes to repaying $161.05 (cash outflow) in five years, this would have been correct. Changing the sign of a number using – or the “minus” key is wrong. Use the (-) instead.
• You don’t have to re-enter all of the data in order to change any of the variables in this problem. For instance, you want to know what the future value is going to be if you left the money invested for 10 years instead of 5. You only need to enter 10 on the N line and find the solution for FV. The answer that you will find is 259.37.

Solving for the Present Value of Lump Sums

The calculations for the present value of a lump sum and the future value is very similar. Don’t forget that the present value will always be less than the future value unless the interest is negative. Keeping this in mind will help you identify wrong answers because of the wrong input. Here’s another problem we can try:

Jim is planning to send his daughter to college in 18 years. He assumed that he will need $100,000 at that time so he can pay for her tuition, room and board, party supplies, and other expenses. How much money will Jim need to invest today as a lump sum to achieve his goal of earning an average 8% annual rate of return per year?

In this problem, here are the facts we already know:

• The future value is $100,000
• The number of periods is 18 years
• The per-period rate is 8% per year

What you need to find now is the present value. To do this, go to the TVM Solver and enter the data as follows:

• 18 into N
• 8 into I%
• 100,000 into FV

Notice that the $100,000 is entered as a positive number because in 18 years, Jim will be withdrawing that amount. The next step is to move to PV and press ALPHA ENTER and you will see the amount of $25,024.90 which Jim will need to invest today in order to meet his goal. You might think it’s a lot of money to invest all at once but later on, you’ll learn to lessen the pain by investing each year in small amounts.

How to Solve for the Number of Periods

There are times that you’re fully aware of how much money you have now and how much you need to have at an undetermined future time period. You can solve the amount of time that it will take for the present value to grow to the future value if you know the interest rate and by solving for N. 

For example, Steph has $1,250 today and she’s interested in finding out how long it will take for her to double her money to $2,500. Her assumption is that she can earn 9% per year on her investment.

Using the Rule of 72, you can quickly approximate this type of problem but if you want to easily find the exact answer, you can use the TI 84 Plus calculator. All you have to do is enter 9 into I%, -1250 into PV, and 2500 into FV. The next step is to scroll up to N and press ALPHA ENTER and you will see that in order for your money to double, you have to wait for 8.04 years. 

Another important thing to note is that entering your number must be based on the cash flow sign convention. You will get ERR: DOMAIN on the screen if you don’t make either the PV or FV a negative number (and the other one positive). The reason why this happens is that positive numbers makes the calculator think that you are getting a benefit without making any investment. In case this error occurs to you, just press 2 (Goto) to return to the TVM Solver and then change the sign of either PV or FV to fix the problem. 

How to Solve for the Interest Rate

Solving the interest rates is especially helpful for people who recently sold an investment and would like to know what their compound average annual rate of return is. Calculating the interest rate is also helpful for people who want to make an investment and would like to know what rate of return they need in order to reach a certain future value. Let’s look back at the college savings problem we solved above but we’ll tweak it a bit.

Let’s say Jim plans to send her daughter to college in 18 years and assumed that he already knows that he will need $100,000 at that time in order to pay for tuition, room and board, party supplies, and other expenses. If Jim is investing $20,000 today, what compound average annual rate of return will Jim need to earn to reach his goal?

Like we previously did, we need to be cautious when entering the PV and FV into the calculator. In this case, here are the things we know:

• Jim is invest $20,000 today which is a cash outflow
• He will receive $100, 000 in 18 years which is cash inflow

This means that we have to enter -20,000 into PV and 100,000 into FV. We need to type 18 into N and then solve for I% in order to get 9.35% average earnings per year. Again, if you didn’t follow the cash flow sign convention, you’ll get ERR: NO SIGN CHNG instead of an answer. You can then press 2 to return to the TVM Solver and have the problem fixed.

Notice that in our original problem, our assumption was Jim would earn 8% per year, and found that Jim needed to invest about $25,000 to reach his goal. In this case, though, we assumed that Jim started with only $20,000. You would, therefore, need to earn a higher interest rate to reach the same goal.

Make sure you give the answer a second look after you solved the problem and check if it’s accurate. You must understand the calculations made by the calculator and the relationships between the variables. If you don’t, you’ll quickly learn that entering the wrong numbers will give you wrong answers. 

PV and FV of Annuities

We previously learned how to look at the basic time value of money keys and how they are used to calculate the present and future value of lump sums. In this section, we will learn how to use the TI 84 Plus to calculate the present and future values of regular annuities and annuities due. 

A regular annuity is an equal cash flow series happening at equally spaced time periods. The first cash flow happens at the end of the first period when it comes to a regular annuity.

An annuity due and a regular annuity is similar except that the first cash flow occurs immediately.

How to Find Present Value of Annuities

For example, Mark decided to make an investment that will pay him $1,000 per year for 10 years. If Mark earns a rate of 9% per year on similar investments, how much would he be willing to pay for this annuity?

What we need to do in this problem is to solve for the present value of this annuity since that is the amount Mark is willing to pay right now. You have to enter the following numbers to their appropriate lines:

• 10 into N
• 9 into I%
• 1000 (cash inflow) into PMT
• 0 for FV

To solve the problem, move to the PV line and press Alpha Enter. You’ll find that the answer is -6,417.6577. As we previously mentioned, the result becomes negative because it represents the amount Jim would have to pay (cash outflow) today so he can buy this annuity.

How to Solve for Future Value of Annuities

For example, Jane borrows $1000 each year for 10 years on a 9% rate and pays back the loan immediately after she receives the last payment. How much will Jane have to repay?

The solution is simple. We just have to put a 0 into PV to clear it out and then solve for FV to get -15,192.92972 (a cash outflow).

How to Solve for the Payment Amount

Solving for annuity payment is oftentimes necessary. If you want to know how much a mortgage or auto loan payment will be or you if you want to know how much money you need to save yearly to reach a particular goal, solving for annuity payment is the only way. We previously used saving for college as an example so let’s use that again, only this time, we’ll look at it as an annuity problem instead of a lump sum.

In 18 years, Jim is planning to send his daughter to college. He already assumed that he needed $100,000 at that time in order to pay for all the college expenses. If Jim thinks he can earn an average annual rate of return of 8% yearly, how much money would Jim need to invest at the end of each year to achieve his goal?

As you may recall, Jim would have to invest $25, 024.90 if he were to make a lump sum investment today. That change is quite huge. Saving for college, in this case, will be fairly easy because the investment is spread over 18 years rather than all at once. 

The data that we will enter is the following:

• 18 into N
• 8 into I% 
• 100,000 into FV

Next, we will solve for PMT which will then lead us to a result of $2,670.21 investment per year for the next 18 years in order for Jim to meet his goal of having $100,000.

How to Solve for the Number of Periods

When you solve for N, you will know the answer to the question, “How long will it take..”

Here’s an example:

John has just retired. He has a nest egg of $1,000,000. For the rest of John’s life, he will be drawing down money from that nest egg. If John expects he will earn 6% per year on average and withdraw $70,000 per year, how long will John be able to afford to live? The assumption here is that John’s first withdrawal will occur one year from today.

The data that you have to enter are as follows:

• 6 into I%
• -1,000,000 into PV (you are investing this amount so it’s negative)
• 70,000 into PMT

The next step is to solve for N which will then result in 33.40 withdrawals. John can, therefore, afford to live for about another 34.40 years assuming that he can live for about a year on the last withdrawal.

How to Solve for the Interest Rate

Finding the I% is similar to solving any other variables. This tutorial mentioned several times that paying attention to the signs of the numbers that you enter into the TVM keys is important. You will get a potentially wrong answer or an error message if you don’t get the signs right when solving for N, I%, or PMT. For solving the interest rate, here’s an example we can take a look at:

Suppose that Helen is offered an investment that will cost $925 and for the next 20 years, will pay her an interest of $80 per year. Additionally, the investment will pay $1000 at the end of the 20 years. What will be Helen’s compound average annual rate of return if she purchased this investment?

In this problem, here are the things we already know:

• Present value is $925
• Future value is $1,000
• Annuity payment is $80 per year

You need to be especially careful to get the signs right as mentioned above. In this case, your cash inflows are both the annuity payment and the future value which means they should be entered as positive numbers. The cost of the investment and the cash outflow is the present value which means it should be entered as a negative number. Note that you will get the wrong answer if you made a mistake by entering the payment as a negative number. Now if you were to enter all three with the same sign, an error message will appear.

Here are the numbers we need to enter:

• 20 into N
• -925 into PV
• 80 into PMT
• 1000 into FV

If you solve for I%, it should give you 8.81% per year as the average return of investment.

How to Solve for Annuities Due

In the previous examples, our assumption was that the first payment would be made at the end of the year which is usually expected. But what if you plan to make or receive the first payment today? The cash will, therefore, change from a regular annuity into an annuity due.

The calculator is normally working in End Mode. The cash flows are assumed to occur at the end of the period. However, in this case, the payments occur at the beginning of the period. So the calculator must be put into Begin Mode. You can scroll down to the bottom of the TVM Solver if you want to change to Begin Mode. You will notice that END is currently highlighted. Highlight BEGIN by pressing the right arrow key and then press ENTER. You’ll see that nothing will change about how you enter the numbers. The cash flows will simply be shifted for you by the calculator. It’s obvious that you’ll get a different answer.

Let’s have a look at the college savings problem but this time, let’s assume that Jim start’s investing immediately:

Jim plans to send his daughter to college in 18 years and he assumes that he will need $100,00 in order to pay for the tuition, room and board, party supplies, and other college expenses. How much would Jim need to invest at the beginning of the year starting today if his goal is to earn an average annual rate of return of 8% per year?

Just like what we previously did, let’s enter the following data:

• 18 into N
• 8 into I%
• 100,000 into FV

Since we are now treating this as an annuity due, just solve for PMT once you changed to Begin Mode. The result should give you $2,472.42 as the amount you need to invest if you start investing today. Because of the extra time for your investments to compound, you get about $200 per year less than if you make the first payment a year from now.

After you solve the problem, make sure you switch back to End Mode. Always practice switching back since you may always find yourself needing to be in End Mode. Next, you have to scroll down to the bottom of the TVM Solver, highlight END and press Enter. 

How to Solve for Perpetuities

We occasionally have to deal with annuities that pay forever (theoretically) instead of for a finite period of time. This type of cash flow is called perpetuity, sometimes perpetual annuity or infinite annuity. TI 84 Plus, however, has no way to specify an infinite number of periods for N, and that could become a problem.

It’s easy to calculate the present value of perpetuity using a formula. We do it by dividing the payment per period by the interest rate per period. The payment is $1,000 per year in our example while the interest rate is 9% annually. If that was perpetuity, the present value would therefore be:

$11,111.11 = 1,000 ÷ 0.09

Did you know that you can “trick” the calculator into getting the correct answer if you happen to forget the formula? Cool, right? You can do this because the present value of a cash flow far enough into the future is going to be approximately $0. This means that the cash flows no longer add anything to the present value beyond some future point in time. We can, therefore, get a very close approximation if we have a specific suitably large number of payments to perpetuity.

Let’s apply this with our perpetuity. Just enter the following data:

• 500 into N
• 9 into I%
• 1000 into PMT

If you scroll to PV and press Alpha Enter, the answer you will get is $11,111.11.

Since the cash flows never end (period infinity never arrives), there will be no future value of a perpetuity.

The third part of this tutorial will involve uneven cash flow streams, net present value, internal rate of return, and modified internal rate of return.

Calculating NPV, IRR and MIRR

So now that we’re done with the basic time value of money keys and have learned how to use them to calculate present and future value of lump sums and regular annuities, it’s time to learn how to calculate the present and future values of uneven cash flow streams using the TI 84 Plus. In this page, we will also learn how to calculate the following:

• Net present value (NPV)
• Internal rate of return (IRR)
• Modified internal rate of return (MIRR)

How to Solve Present Value of Uneven Cash Flows

You might find it more difficult to use the TI-84 Plus here than most other financial calculators. However, once you get used to it, it will no longer be as hard. Let’s get started by exiting from the TVM Solver menu and pressing 2nd MODE and then pressing APPS, then return to the finance menu.

We need to use the NPV function if we want to find the present value of an uneven stream of cash flows. The definition of this function is:

NPV( Rate, Initial Outlay, {Cash Flows}, {Cash Flow Counts})

Remember that the {Cash Flow Counts} part is optional and we won’t deal with it here. 

If for example, Malcolm is offered investment and at the end of the next five years, it will give him the following cash flows:

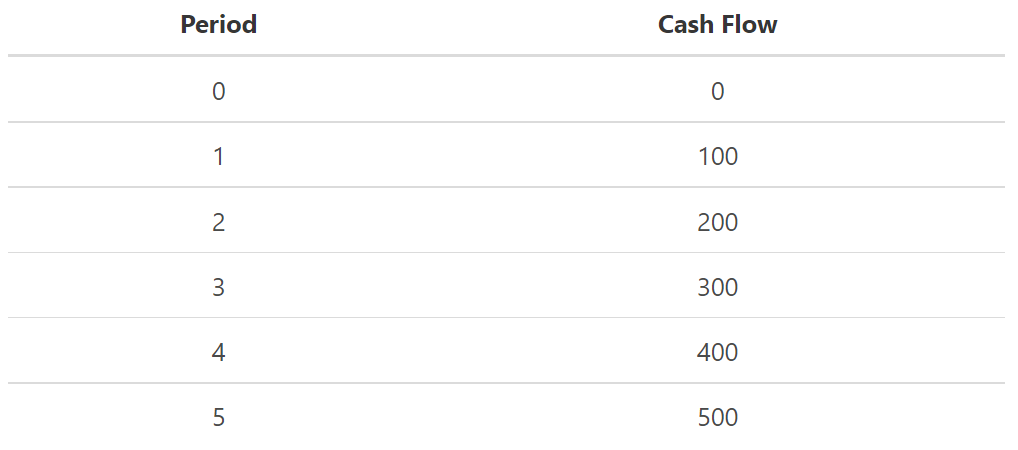
If Malcolm’s assumed rate of return is 12% per year, how much would he be willing to pay for this investment?

To solve this problem, we have to find the present value of each of these cash flows. We will do it individually and then we will sum up the results. But this route can be hard. What we can do instead is to use the NPV function. Let’s start by scrolling down in the finance menu until we get the line that reads NPV(. To select that function, just press Enter and the beginning of the NPV function will appear on the screen. We will then complete the function like this:

NPV(12,0,{100,200,300,400,500})

As soon as we press ENTER to solve the function, the present value should be $1,000.17922. Remember that if you press the 2nd Enter, we can easily change the interest rate because we retrieved the function, and then we can edit it by using the arrow keys. 

Here’s an example: 

Change the rate to 10% by pressing 2nd Enter and then use the arrow keys to transfer to the interest rate and press DEL to delete the 12. You will then press 2nd DEL which is the INS function and then enter 10. You will find that the answer is now $1,065.25883 once you press Enter. Before you continue, make sure you reset the interest rate to 12.

How to Solve Future Value of Uneven Cash Flows

In order to find the future value of these cash flows instead of the present value, we will need to use a bit of genius approach since there is a function to do this. Note that one way to find the future value of any set of cash flows is to first solve for the present value. The next step is to find the future value of that present value and that’s how you can get your solution. 

In this case, we already know that the present value is $1,000.17922. We will then recall the NPV function by pressing 2nd Enter (pressing this twice might be necessary to get back to the original 12% interest rate). Next, let’s add * 1.12 ^ 5 to the end of the function. The end result will be:

NPV(12,0,{100,200,300,400,500})*1.12^5

Once you press Enter, $1,762.65754 will appear as the future value of these cash flows. Well, that was easy! At least easier than adding up the future values of each of the individual cash flows. It will, however, require you to know the equation for the future value of a lump sum but that’s something you already know anyway.

Solving for Net Present Value (NPV)

When you calculate the net present value (NPV) and/or internal rate of return (IRR), you will find that it’s kind of similar to solving for the present value of an uneven cash flow stream as we have done in Example 3. 

If you were offered the investment in Example 3 at a cost of $800, what would your NPV and IRR be?

To solve this problem, here are some things to keep in mind:

• The calculator must not only have the annual cash flows but the cost as well. Remember that we set the cost to 0 since we only needed the present value of the cash flows.
• In general, an investment must be paid first before you can receive its benefits so the cost or the initial outlay is said to occur at a time period (today for example).

We will find the NPV by recalling the NPV function and editing it so that the initial outlay becomes -800. This is how the function is going to look like on the screen:

NPV(12,-800,{100,200,300,400,500})

You will get the solution by pressing Enter. The answer will then be $200.17922 as the NPV.

How to Solve Internal Rate of Return

Finding the IRR is done the same way as above except that we’ll use the IRR function. The definition of this function is:

IRR(Initial Outlay, {Cash Flows}, {Cash Flow Counts})

For this problem, the function is:

IRR(-800, {100,200,300,400,500})

Again, we will ignore the {Cash Flow Counts} because it’s optional. 

We have to press APPS, return to the finance menu, and scroll down until we see the IRR(. We will enter the function as shown above and then press Enter to get (19.5382%) as the answer.

How to Solve the Modified Internal Rate of Return

Since it’s simple and can be interpreted, the IRR has been a popular metric for evaluating investments for many years. However, there are some serious problems with the IRR. One of its problems is that it completely assumes that the cash flows will be invested again for the life of the project at a rate that equals the IRR. A project that is considered good may have an IRR that is significantly greater compared to any reasonable reinvestment assumption. This is why at times, the IRR can be misleading.

In order to solve this problem, the modified internal rate of return (MIRR) may use a straightforward reinvestment rate. The issue here is that financial calculators don’t have a MIRR key as they have in the IRR key. So we will have to use a smart approach to calculate the MIRR. Good thing it’s not difficult. We will use the following steps in the algorithm:

We have to calculate each of the cash flows’ total present value starting from period 1. Don’t forget to set the initial outlay to 0. Just like we did in Example above, we have to use the calculator’s NPV function. We will find the present value by using the reinvestment rate as your discount rate.

Next, we have to calculate the future value as of the end of the project life of the present value from step 1. We will use the reinvestment rate as our interest rate to find the future value.

Lastly, we will look for the discount rate equal to the initial cost of the investment with the future value of the cash flows. MIRR will be the discount rate which can be interpreted as the compound average annual rate of return earned on investment if you invest the cash flows again at the reinvestment rate.

Now, let’s say you were offered the investment in Example 3 at a cost of $800 and in the reinvestment rate is 10% per year, what will your MIRR be?

Here’s a step-by-step procedure when going through our algorithm:

Example 3 shows the present value of the cash flows.

NPV(10,0,{100,200,300,400,500})

We will discover that the present value is $1,065.26.

In order to find the future value of the cash flows, here’s what you need to do:

• Go to the TVM Solver and enter 5 into N
• 10 into I%
• -1065.26 into PV

When you solve for the FV, you will get $1,715.61 as the answer.

The problem has now been transformed into an $800 investment with a lump sum cash flow of $1,715.61 in period 5. The discount rate (I%) that equates these two numbers is the MIRR. If you enter -800 into PV and then solve for I%, you’ll get 16.48% per year as the MIRR.

Remember that we can combine steps 1 and 2. We can calculate the future value using our 10% reinvestment rate as we did in Example 3 like this:

NPV(10,0,{100,200,300,400,500})*1.10^5

Similar to what we found above,  $1,715.61 is our future value. Let’s go to the TVM Solver this time and enter 5 into N, -800 into PV, and into FV enter 1715.61. When you solve the I%, you will get 16.48% as the MIRR just like before.

So now, we found out that at a cost of $800, our project is acceptable. We found that the NPV is positive, the required return is 12% which is less than the IRR, and the required return is 12% which is lesser than the MIRR.

Solve Non-Annual Periods on TI-84 Plus

Annual time periods is probably one of the most used calculations in the real world. For instance, most consumer loans need monthly payments such as mortgages, car loans, and credit cards. In fact, we have used annual time periods in all the previous examples for simplicity. Now, it’s time to dive through the non-annual problems.

Considerations

You must understand all the annual problem principles you have learned still apply for non-annual problems. Nothing has changed at all, actually. You’ll understand it better if you think in terms of “periods” rather than years. Any amount of time can be a period. Daily, monthly, quarterly, semiannually, or annually are the most common. A time period, however, can be any imaginable amount of time.

You must first consider the number of periods in a year when dealing with non-annual periods. This is because consistency in entering data into the 84 Plus is important. Whatever numbers you enter into the N, I% and PMT keys must agree as to the length of the time periods you used. Therefore, if you are dealing with a monthly problem, then the total number of months should be your N, the monthly interest rate should be you I%, and the monthly annuity payment should be your PMT.

Example

It’s very common for you to face a problem that involves annual numbers but then told that “payments are made on a monthly basis,” or that “interest is compounded daily.” You must, therefore, adjust the numbers given if you ever face this kind of problem. Let’s have a look at this example:

Leo is thinking about buying a new home for $250,000. Leo was told by his banker that they are willing to offer him a 30-year fixed-rate loan at 7% with monthly payments. What will Leo’s required monthly payment be if he borrows the entire $250,000?

From that problem, here are the things we know:

• The loan term is 30 years
• Interest rate is 7% per year (merely implied, not stated explicitly)

In this case, you might be forgiven for expecting that a period is one year but you will, later on, learn that the payments must be made every month. This means the length of a period is one, and in order to get the correct answer, you must convert the variables to a monthly basis.

We calculate the total number of periods by multiplying 30 years by 12 months per year (since there are 12 months in a year). This means that N is 360 months and not 30 years. Similarly, when you divide the 7% annual rate by 12, you get 0.5833% per month as the interest rate. Since it occurs at a single point in time, not repeatedly, we will not make any adjustments to the PV ($250,000). If there was an FV in this problem the same logic would apply. The calculator will give you the monthly payment amount automatically (per period to be exact) when you solve for the payment.

In this problem, we have to enter 360 in N, 0.5833 into I%, and 250,000 into PV to solve for the payment amount. The monthly payment will be $1,663.26 when you solve for PMT.

Rounding is another thing you need to be cautious of. For instance, you should do the calculation in the I% line in the TVM Solver when calculating the monthly interest rate. It’s wrong to do the calculation and then write down the answer for a later entry. Doing this will shorten the interest rate to the number of decimal places that appear on the screen and your answer will be impacted by the rounding. It doesn’t matter whether the difference only involves a few pennies, every penny matters. If you really want to see what happens, try sending your lender a payment that is consistently three cents less than required. We bet you’ll get a nasty letter the next day. 

Things to Remember

If you think it’s okay to treat the problem as an annual one and then, later on, adjust your answer to be monthly, then you’re wrong. Mathematics doesn’t work that way. If you want proof, try to input annual numbers, and then convert the annual payment to monthly by dividing by 12. Next, enter 30 into N, 7 into I%, and 250,000 into PV.  You will find that when you solve for PMT, the answer will be $20,146.60. However, monthly payments must be made so if we divide that by 12, a monthly payment of $1,678.88 appears. 

As you can see, if the problem is solved this way, you’ll get a $15.63 answer every month which is too high. Therefore, you must always adjust your variables before solving the problem. The compounding of interest is the reason why there’s a difference. The more frequently interest is compounded, the smaller the payment needs to be for it to grow to a specific future value.

TI-84 Plus Payments per Year Setting

You probably noticed that by using the P/Y setting at the bottom of the TVM Solver, the TI 84 Plus can semi-automatically adjust for payment frequency. For situations where the compounding frequency is different from the payment frequency, it can also be adjusted by using C/Y. This feature, however, causes more problems than it solves. It’s because when you do the next problem, you will more likely forget to change it and will probably get the wrong answer. This setting can give you problems that cannot be easily identified.

Let’s discuss how to use this setting anyway. 

If for example, you set the P/Y value or “payments per year” to 12, the calculator will assume monthly compounding and appropriately adjust the interest rate. However, the number of periods or the payment amount will not be adjusted by it and take note, this is very important. This is what makes the feature worthless. 

C/Y, on the other hand, means “compounding periods per year” and is normally similar to P/Y. If you change P/Y you will find that C/Y will also change to the same value. If the compounding frequency differs from the payment frequency, C/Y can be changed. For instance, the interest rate of your quarterly payments is compounded monthly, you would then set P/Y to 4 and C/Y to 12.

Now, let’s do the problem again. This time by using this feature:

1. First, set P/Y to 12 (monthly)
2. Enter the data: 360 into N (again, you still have to enter the total number of periods), 7 into I%, and 250,000 into PV.
3. Next, let’s solve for the payment by pressing Alpha ENTER. The answer will be $1,663.26 as the monthly payment.

As you can see, we got the correct answer but we didn’t save anything at all by using that “shortcut.” What actually happened was that it took an extra keystroke or two to use this feature. Additionally, you will get the wrong answer if you forget to change the setting when you do the next problem. Unless of course the problem also happens to use monthly compounding.

We highly recommend that you follow the simple steps outlined above. Just set P/Y to 1 and you don’t have to think about it anymore. Always make the total number of periods as the N, the interest rate per period as the I%, and the payment per period as the PMT.

Frequently Asked Questions

Can you explain the optional [cash flow counts] part when using the NPV and IRR functions?

The purpose of that feature is to save some data entry in specific situations. It’s also an identical purpose to the frequency prompt in several other calculators. You can include the “cash flow counts” array if you find that some of your cash flows repeat. For instance:

If the discount rate is 8% per year, what will the present value of the following series of cash flows be?

100, 200, 200, 200, 300.

This problem is usually solved through the NPV function as follows:

NPV(8,0,{100,200,200,200,300})

However, as you can see, you will be required to type “200” three times in a row. We can do it like this when you use the “cash flow counts” array:

NPV(8,0,{100,200,300},{1,3,1})

Either way, you’ll get $774.01 as the present value. But you won’t have to put in too much effort typing and the chance of getting data entry errors is lesser. In this example, it doesn’t really save much time but in terms of other problems, it can.

Why does my TI-84 Plus manual say we have to use lists in the NPV and IRR functions, yet you never use them?

It’s because we want to create on the fly arrays the quicker and easier way instead of using lists. Also, we don’t recommend you to reuse a list more than once or twice. If you do end up reusing it, just use the editing functions to get it done quickly.

I’m getting an error when I use the NPV and/or IRR function. What’s happening?

There are different reasons as to why this is happening. Typically, it’s because someone is not being careful in doing variable separation in the function by commas. It is absolutely necessary to use every comma you see. Another reason why this happens is that you neglected to make the initial outlay a negative number. When using the TVM Solver or the functions, you must obey the cash flow sign convention.

Is it possible to calculate the number of days between two dates using the TI 84 Plus?

Yes. There are two date formats supported by TI-84 Plus. They are MM.DDYY or DDMM.YY. Use the dbd (days between dates) function from the Finance menu when calculating the difference between two days. For instance, get the number of days between 25 July 2007 and 31 December 2007 by typing:

dbd(08.2507,12.3107) if you are using MM.DDYY

or

dbd(2508.07,3112.07) if you are using DDMM.YY

Whichever way you do it, the answer you will get is 128 days between those two dates.

Remember that you cannot specify a day count basis when using the TI 84 Plus. The basis will always be actual/actual.

Is there any other way to find roots other than using square roots of the TI-84 Plus?

It may seem like calculating various roots is all we do in finance. The good news is that it’s actually very simple to do. You only need to remember simple mathematical rules.

In order to calculate the 5th root of 100, just raise 100 to the 1/5th power. You can do this in the TI-84 Plus by typing: 100^(1/5) ENTER. The 5th root of 100 is equal to 2.51189 in this example. Keep in mind that the parentheses are necessary otherwise you would raise 100 to the 1st power, divide by 5, and the answer you will get is 20. You can calculate any root using this strategy.

I only have a key to calculate natural logarithms in my calculator. How can I calculate logarithms to other bases?

We would usually use natural logarithms (base e) in finance which is typically abbreviated as Ln(x). But there are times we need to use other bases. You can covert base e to any other base by doing the following formula (say we are converting to base 10):

Log10(X)=Ln(X)Ln(10)

Thus, you can compute the natural log of your number and then divide it by the new base’s natural log. For instance, Log10(3) = Ln(3)/Ln(10) = 0.478. If you want to calculate base 10 logarithms, you can do so by using the LOG key of TI-84 Plus.

What should I do to clear the memory of all variables and lists?

It’s actually easier and safer to do the following compared to a complete reset:

• Press 2nd MEM (that is the second function of the + key)
• Select 2 (Mem Mgmt/Delete)
• Select 1 (All)
• Scroll through the list and delete anything that isn’t important using the DEL button.
• To exit, press 2nd QUIT.

Just remember to be careful not to delete any lists or variables that you need to save.

I want to completely reset my TI 84 Plus back to the factory default settings. How can I do that?

Be careful when resetting because it will remove any programs that you may store in the calculator. This is how you can reset it:

• Press 2nd MEM (that is the second function of the + key)
• Choose 7 (Reset)
• Scroll right so that ALL is selected
• Press 1
• Press 2 (Reset, and read the warnings)

Keep it in mind that resetting may impact the contrast of your screen. If you really have to reset, then you can change the contrast of the TI 84 Plus screen by pressing the 2nd and then the up arrow or down arrow button. There are times you will be required to do this repeatedly.

FAQs

1. Does TI-84 plus have financial functions?

Yes, the TI-84 Plus system is equipped with financial functions which makes it more suitable for finance applications.

2. What functions does TI-84 plus have?

The TI 84 Plus system comes with many useful functions that are very similar to other calculators but has some that are specific to finance.

3. What does TVM solver mean?

TVM Solver is short for Time Value of Money. It is a tool that allows you to calculate the interest rates, number of periods and future value of money.

4. How do you use the financial app on a TI-84 plus?

The TI-84 Plus financial app is very simple to use. You can access it by pressing the APPS key and then scrolling over to the F3 icon. The only difference between this and other apps is that you need to input the current interest rate when asked for "Rate".

5. What can I do with TI-84 plus?

With the various built in functions of the TI 84 Plus, it could be used for many different things. You can use it for personal finance or run business applications. The possibilities are endless!